Degrees

Are you one of those people that graduated "summa cum laude" from college?  Would you be able to tell me what "summa cum laude" means?  Because it really just sounds like a retarded black guy informing me that "the current summer's semen ejaculations are excessively noisy."  Drawing an analogy to the banking bonus, summa cum laude for college graduates is the equivalent of "top bucket" in an analyst class, followed by magna cum laude, then cum laude, and lastly all the losers that don't get bona (I know, I know, the economy...).  And yes, "bona" is the appropriate plural for "bonus," and should be a daily reminder that every Latin-based term in popular use could just as easily come from a '70s black porno.

What kinda degree you got?

So for any of the people that throw around "cum laude" or some variation without knowing the meaning, here you go: "cum laude" is the latin term for "with honor."  And that explains why those that graduate "with honors" do so "cum laude."  Make sense?  It should, since loud ejaculations are how every man becomes honorable in college.  I just don't even want to know what my black readers (they exist!) have to say about this.

I raise the topic only because a CFO recently asked me whether I have a Ph.D. in Excel, which eventually led to him asking whether I have any types of cum on my undergraduate degree.  No, but that would probably change if I left my degree out while you watch me awesomely build a 5-year quarterly model in only a few minutes.

Anyway, today's lesson is short.  The DEGREES function converts radians into degrees.  So you can do quick conversions using =+DEGREES(a*PI()), where "a" is any number.  Maybe you'll get lucky and be able to use it on a sell-side for these guys.  Sorry, tomorrow's post will be more educational.

And, just remember, if someone brags to you that they graduated "cum laude," that's like bragging that they won a bronze medal or other type of third place (shit) distinction.  Good thing these types of events aren't done "to-the-death," otherwise we would never experience the pleasure of people bragging about 2nd and 3rd place.

TSM,

-F-One

Depreciation

Apologies for the delay inbetween posts.  Over the past few days, I have been doing far more meaningful things, like reading about this Capital Grille chef who stole customers' credit cards to fund his toy car hobby.  WTF?  How do you do something like cook steak (awesome, manly) but at the same time collect toy cars (creepy, childlike, possibly to bag kids)? Good thing he's out of work now; I've gone ahead and done everyone a favor by registering him here.  Hopefully he doesn't get hired at another Capital Grille where he might decorate my lobster mac and cheese with more than the four requisite cheeses.

Unrelated: in college, my first accounting professor had a peculiar middle-America accent that caused him to pronounce "depreciation" as "deprishiation."  I don't have much meaningful to say about to him, but realized this is my only chance to mention how annoying that SOB was, since today's post is about depreciation. 

First off, those of you that read about my distaste for CPDS' may have also closely read the keyboard shortcuts and noticed the SYD function on the bottom right-hand corner.  SYD stands for "sum of the years' depreciation" (read more about it here, because I don't feel like writing an accounting lesson) and is an alternative to the straight-line method that allows for a greater amount of depreciation in the early years of using an asset.  If you had asked me what SYD is prior to a couple of weeks ago, I could have only told you about a guy I know from Queens, but now I can tell you it's an excel formula written as follows: SYD(cost, salvage, life, period).  Which goes to show how shitty my education from Professor Deprishiation was.

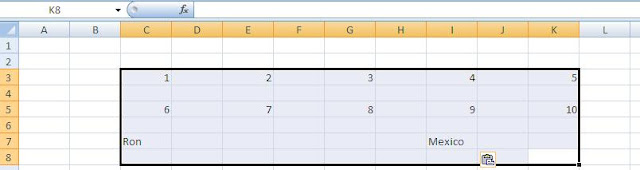
Stepping back (I bet you heard someone say this today) from SYD to depreciation more broadly, you have probably spent some time learning about how to build out depreciation for any new capital expenditures in a model.  The most common method I have seen is the use of a "waterfall;" assuming you project five years in your model, there would be one line showing annual depreciation for the first year of capex, another line for the second year, and so forth.  So let's look at a simple straight-line case:

For every year (or period) of capital expenditures, you add another row to show the depreciation amounts in each ensuing year.  In the above example, these rows are totaled in row 21 to show the total depreciation amount (for new capital expenditures, only).  It's quite the bitch to update the depreciation waterfall anytime you change an assumption on timing (like 5 years to 4 years) or add another year into the projections (thus requiring another row to be manually inserted).  Even if you have automated your formulae to adjust for timing assumptions (as rows 14-19 in this spreadsheet are), you cannot avoid adding another row if you are extending these projections out to 2015.

The solution is to write a formula in one line that accounts for all of these assumptions dynamically; in other words, have a depreciation waterfall built up in one row of a spreadsheet.  Here's how (based on the example above):

1. Use rows 9-12 as assumptions
2. In cell G23, enter the formula =+SUMPRODUCT($G$10:$M$10,1/$G$11:$M$11,IF($G$6:$M$6<=G$6,IF($G$12:$M$12>G$6,1,0),0)) followed by ALT + SHIFT + ENTER
3. Drag the formula in G23 to L23
4. Don't forget to enter in a number (any number is fine) in cell M11 to avoid dividing by zero in your calculation

The above method is obviously an array formula, where calculations are done using corresponding cell ranges of equal size; so the SUMPRODUCT function is really operating as G10 x (1/G11) x a + ... + M10 x (1/M11) x a, where "a" is an operator that determines whether each depreciation amount should be counted for the current time period (the current column). 

The logic for "a" is based on the year of the given capital expenditure and its last year of depreciation.  So, if G10 x (1/G11) is based on a capital expenditure from year 1 (column G) that depreciates through year 5 (column L), then "a" will equal the number 1 in each of those years.  Otherwise, "a" will be 0, which multiplies against the depreciation amount to make it zero, thus excluding it from the depreciation total.  A good example of how this calculation works can be found in K14 through K19.  If K14 belongs, our SUMPRODUCT formula multiplies it by 1, and if not, then by 0.  Thus the SUMPRODUCT formula is doing the work of the SUM formula in row 21, in addition to the calculations for the depreciation waterfall directly above.

Thus, you now have the ability to insert another year in your model, and allow for depreciation to be calculated precisely in one line, based on the assumptions you enter and without the need for manual adjustments.

So why have I not told you anything about sum of the years' depreciation, even though it's just calculated in the same waterfall format with different numbers for different years?  To be honest, it's complicated as shit to write a dynamic formula into one line.  So here it is for cell G23: =+SUM(IF($G$6:$M$6<=G$6,IF($G$12:$M$12>G$6,SYD($G$10:$M$10,0,$G$11:$M$11,IF($G$9:$M$9+IF($G$9:$M$9>F$9,-1*F$9,RANK($G$9:$M$9,$G$9:$M$9,0)-RANK(G$9,$G$9:$M$9,0)+1-$G$9:$M$9)<=$G$11:$M$11,$G$9:$M$9+IF($G$9:$M$9>F$9,-1*F$9,RANK($G$9:$M$9,$G$9:$M$9,0)-RANK(G$9,$G$9:$M$9,0)+1-$G$9:$M$9),1)),0)),0)

I'll explain it some day when I feel like it.

-F-One

Modeling Framework

I used to have a superior (in title only; he was a dumbass) that commonly used the phrase, "level-set."  As in, before we go any further, let's do some level-setting with a 30,000 foot overview.  Because, you know, commercial airline pilots always use construction tools.  He really was a dumbass.  Anyway, taking a page out of his dumbass playbook, I'm using this post to do some level-setting of my own with regard to financial modeling and all of the important pieces.  Thereafter, I can use future blog entries to heavily rain down Excel knowledge for your continued benefit.

Most readers have familiarity with the basic layout of a financial model.  For those lacking that familiarity, let me borrow a trick from crappy resume-writing and just tell you the objective: to show a company's income statement, balance sheet and cash flow statement projected into the future, with the ability to change assumptions for various accounts and display their impact on each of the statements.  So let's start with the basic framework of a financial model, which a VP once told me is not much different from a fine-tuned automobile:

1. Steering wheel (controls / assumptions)
2. Axes and tires (formulas / financial statements)
3. Interior furnishing/paint job (formatting)
4. Higher likelihood that Asian females would crash it (ditto)

Does this also mean Asian males would soup up their models with "Toyota Racing" decals and nitrous oxide engines?  Cause that might be 2 fast, 2 furious.

How much do you think your dream car would skimp on any of the above-mentioned items?  If it does at all, then improve your imagination.  You can't have a shitty steering wheel or axes if you want your car to get around and change directions.  You also don't want paint peeling off the side doors.  And if it's Asian-chick-proof, it's not a car, it's a cement block (assuming they don't know martial arts).  By the way, why do car salesmen say "side doors" when talking about sedans? All doors are on the F'ing side.  Front and rear doors?  I don't see anyone climbing into their seats through the hood.

But enough nonsense.  For a model to work mechanically (disregarding how realistic the numbers may be), you need acertain number of inputs (they only need to be numbers to start off), and the rest of the model will all be calculations based on these inputs.  At the most advanced levels, these inputs become models within themselves, driven by many underlying functions and assumptions.  For example, a basic model may show revenue as $100 million for each of the next five years.  However, a slightly more advanced model will show revenue as a function of annual growth percentages.  Further, a complex model may show revenue as a function of several individual customers or accounts, with each based on numerous assumptions for price, volume, market size, etc.

So here is the basic framework, along with which inputs will drive the model.  Again, many future posts will be dedicated to transforming these numbers into more complex, functional formulas.
Income Statement 

1. Revenue - COGS - operating expenses = operating income
2. Operating income + interest income - interest expense = pre-tax income
3. Pre-tax income - taxes = net income

Balance Sheet:

1. Assets = cash + current assets (accounts receivable, inventory, prepaid expenses, etc.) + long-term assets (PP&E, etc.)
• Cash = previous year's balance + net cash flow
• PP&E = previous year's balance + capital expenditures - D&A
2. Liabilities = current liabilities (accounts payable, deferred revenue, etc.) + debt + long-term liabilities
• Debt = previous year's balance + debt issuance - debt repayment
3. Shareholders' equity = 
• Retained earnings = previous year's balance + net income - dividends
• Share capital (is this what you call it? I got fired from an accounting internship) = previous year's balance + stock issuance - stock repurchase
4. Assets = liabilities + shareholder's equity

Cash Flow Statement

1. Cash flow from operations = net income + D&A - increases in working capital
2. Cash flow from investing activities = - capital expenditures
3. Cash flow from financing activities = debt issuance - debt repayment + stock issuance - stock repurchase - dividends
4. Cash flow from operations + cash flow from investing activities + cash flow from financing activities = net cash flow

If you happened to read this far, you're more of a loser than I am for writing this far,

-F-One

What You Need to Know About Keyboard Shortcuts

In today's New York Post, I saw this article describing the acrimonious departure of a female cook from one of Jean-Georges' restaurants.  The cook recently filed a sexual harassment lawsuit, and as in all such cases these days, the defendant "went so far as to text her a picture of his manhood."  At the risk of accusations that I think about this topic frequently, I am totally confounded by the picture-messaging of manhood becoming a rapidly growing trend (at least in professional sports).  Just in the past year, Brett Favre, Martellus Bennett and Greg Oden, among others, have all been accused.

They should call them Wang-ler jeans.

What the hell?  Whatever happened to calling/texting a girl? Why do people engage in this nonsense?  Who even enjoys it (other than this guy)?  Let's assume that your target girl is head-over-heels obsessed with you. What exactly do you gain by sending a cell phone shot of your unit to her? It's not like her cell phone shapeshifts into your dong when she opens up the picture, so the chances that she'll enjoy it are minimal.  Thus, let's assume the other possible scenario that the girl is NOT head-over-heels obsessed with you. No matter how well-equipped you are, at least one of these outcomes will befall your dong photo: 1) topic of ridicule among her friends/coworkers, 2) topic of ridicule among your friends/coworkers, 3) police evidence.  There are no winners in autophallography.

So what do dongs have to do with Excel, you ask? Nothing, unless you use your dong to type. But I recently experienced the Excel equivalent of receiving a CPDS ("cell phone dong shot"), which was a reader sending in a photo of keyboard shortcuts taped to their cubicle.  Why do I even bother to make the comparison?  Like I said, the CPDS doesn't help the girl because the phone isn't morphing into a penis.  Likewise, keyboard shortcuts on the page aren't typing themselves out for you.  In order to get any benefit from shortcuts, you must have full, immediate access to them.

=IF(dongshot=1,0,1)

This is the end of the entry, and you've learned nothing meaningful about Excel.  The next post will be overly bland and information-filled to compensate.

-F-One

Dating in Excel

You might think this entry is about the time I tried to pick up Mrs. F-One with some cool OFFSET formulae.  But it's not.  I'm just trying to exhaust every known Excel pun in the universe, and I'll warn you that there's another one coming before this post ends.  The "dating" to which I refer is actually the labeling of time periods in models, so 2009, 2010, 2011, etc.  For example:

These are dates?  They tell me nothing!

This is how you lay out dates in your model if you are a child that colors with crayons.  By the way, if you watch a lot of TV, you have probably seen some ads for the movie Ramona and Beezus, during which Ramona gets props for "coloring outside the lines."  Supposedly that saying is analagous to creativity or being a free spirit, but what the hell does it even mean?  Regardless of your personality/disposition, if you fully color an entire illustration, don't you NEED to color outside of the lines in order to reach every area of the page?  Or does it mean scribbling colors wrecklessly and ignoring the lines that separate distinct objects and different colors?  Sure, maybe you color that way and happen to be a free spirit, but the only thing it actually guarantees is that you suck at coloring, and might be developmentally handicapped.

In next summer's sequel, Ramona hides from her Asian foster parents, who decide her inability to color "within the rines" has earned her bitch ass two months at math camp.

Let's move beyond the crayon age.  Your computer's microprocessor performs billions of operations per second, so try letting it do a bit more than count from 2009 to 2015:

1. In cell B6, enter the number of months per projection period (obviously 12 for an annual model and 3 for a quarterly model)
2. In cell B7, enter the last date for which actual/historical numbers are available (12/31/09 for simplicity)
3. Starting in cell F6, enter in the first time period in your model (12/31/09 is fine), with custom number format mmm dd,
4. In G6, enter the function =+EOMONTH(F6,$B$6); this function automatically returns the last day of a given month in a given year based on an input date and a specific number of months following the input date
5. Drag the formula in G6 through to L6
6. In F7, enter the function =+YEAR(F6)&IF($B$7>=F6,"A","E"); the YEAR function identifies the year number of a given date, and the IF function determines whether the projection period is historical/actual (A) or projected/estimated (E)
7. Drag the formula in F7 through to L7

Why do we set up the dates in this way?  One reason is that you can easily show the fiscal year end (not always 12/31) for a given company, and which dates are actual vs. estimated, without having to manually adjust any of the labels.  You also have a good way to easily produce annual or quarterly dates in a model.  Further, using the EOMONTH function ensures that you precisely calculate the last day of any given month, rather than occasionally erratic calculations (December 30, anyone?) if you simply add 365 or 365.25 to the last date.  Lastly and most importantly, listing the actual end dates for each period will allow you to do lots of date-relative calculations in your models, which will be discussed in future posts.

The format I've suggested above is not the ultimate date format for financial modeling, but should provide you a base to add further bells and whistles.  It will also prevent your seniors from victimizing you with annoying questions like, "Which periods are actual?" and, "What is the fiscal year end?"  Or as the senior bankers might threaten you, "WHAT IF YOU SHOWED THIS TO A CLIENT?!?!"  After all, clients have been known to open every pitchbook and instinctively identify minorly unclear date formats.
 
Sounds like a lot of fun right?  If you think dating in Excel is fun, just wait until the lesson on punishing!
 
-F-One

Custom Number Formatting

Anyone that has worked on a client pitchbook for banking or an investment committee memo for private equity knows that formatting is of the utmost importance (some might say gross overimportance).  I can't speak for hedge funds, but I have a friend that proudly works at a health care hedge fund, and believes that formatting is for people who don't have a real job like him.

I'd rather not debate who has a real job or whether formatting is important or not, but let me give you some words of motivation on why I even attempt to format spreadsheets and presentations.  When I suffered Training the Street (are all these references a delayed onset of Stockholm Syndrome?), our instructor Scott threatened all bad formatters by saying, "Watch out, I am an anal monster."  Yeah.  Of course you are.

So some of you may be interested in what an anal monster does or who among your coworkers are anal monsters, but I just assume that everyone is one and that nice formatting can prevent me from finding out anything more.  For this particular post, let's talk about nice formatting in terms of number formats, starting with CTRL + 1, ALT + C, END, ALT + T:

I will assume you know the basics on formatting dollars in millions, with negative numbers in parentheses (rather than with a "minus") and one or two decimal places of significant digits.  If you're already doing this formatting with custom formats, then great; otherwise, read closely to find out what you've been missing.  In the "Type:" field of the "Number" format menu shown above, number formats are entered as: a;b;c where "a" represents positive numbers, "b" represents negative numbers, and "c" represents zero.  You can thus apply some of the following format types:

1. $#,##0.0_);($#,##0.0);"-" for dollars: The #'s ensure that if you enter the number 1.1, it will show up as $1.1 (not $0,001.1) but a number in the thousands or above will still have a comma separating every three digits.  Moreover, zero will appear as a dash, and not "0;" this is more of a personal preference to eliminate seas of zeros that sometimes make extensive models hard to read, and also to allow easy recognition between an absolute zero and a very small number like 0.001 that appears as 0.0.
2. $#,##0.0_);[RED]($#,##0.0);"-" for dollars with negative numbers automatically colored red: Basic colors like [RED] and [BLUE] work in the customer formatting framework when in brackets and preceding an expression.  You can also try [TURQUOISE], but that would make you an idiot.
3. #,##0.0x_);(#,##0.0x);"-" for multiples
4. #,##0.0%_);(#,##0.0%);"-" for percentages
5. "Yes";;"No" for binary code: Excel also has TRUE and FALSE built into the program as 1 and 0, respectively.
6. "" or ;;; to make cells blank
7. mm/dd/yy for dates: Other formats that work include mmm dd, yyyy or mmmm dd or some combination.  I have no idea how this follows the positive;negative;zero rule.

You get the idea.  And you have probably figured out by now that you can also format a number using one of the preset options, and later toggle to the custom option to see the code.  The possibilities are limitless.  Just don't use that stupid accountant format where you right align a number and the dollar sign is still all the way to the left.  If you do use it, why don't you try writing out the number 1,000 as 1,                  000?  Maybe that will satisfy your urge to make documents as illegible as possible.

Last thought: does an anal monster enjoy "anus" or "ani?"

I work for TTS and enjoy the plural of anus 

Helpful,

-F-One

Need for Speed

How fast can a human being possibly use Excel?  This is not an easy question to answer.  However, it's frequently a very important question to the younger people that work in investment banking, PE or hedge funds, because much of their livelihoods are tied to Excel.  Particularly in banking, the faster your execution speed is overall, the less miserable life becomes.  Speaking of miserable, for the week that I was exposed to Training the Street, they introduced us to their version of the "Excel speed test," which was a formatting exercise typically completed in a minute, but sometimes completed as quickly as 30 seconds.  I never finished it, so you could probably call me slow.

Regardless, I do know a thing or two about speed relative to Excel. Here is what it takes:

How fast (or slow) of a typist are you?

1. Typing speed - If you can't type at least capably, you can give up any hope of using Excel any faster than that old MD that doesn't check e-mails or use Excel since he started working before computers and high-yield debt existed. Typing speed is like the 40-yard dash for football players: raw speed. You could type 130 WPM (probably equivalent to a 4.2 second 40), or you could only type 50 WPM (offensive lineman speed). Anything below that range, and you should probably consider changing professions.
2. Shortcut/function knowledge - Even if you are the greatest typist in the world, you can't do much financial modeling (at least quickly) without knowing your way around Excel.  This is the same reason track stars cannot always be great football players; speed is no guarantee that they know the playbook and how to play (think of John Capel vs. Randy Moss).  So for maximum speed, you need to know things like CTRL + 1, CTRL + arrow keys, etc.  Having the ability to type out a Steven King novel in a couple of hours may help, but not much since you aren't writing novels in the spreadsheet.
3. Brainpower - Some might argue that this is tied to typing speed, which is partly true, but I want to highlight the importance of a good memory, quick recall function, etc.  You may have posted on the side of your cubicle (a good Asian friend of mine used to call it a "cubic") a sheet listing commonly used keyboard shortcuts.  Does this help you?  Maybe, but certainly not in significantly increasing your speed.  If you just transitioned from Excel 2003 to 2007 and are looking for the command for "Page Setup" (ALT, P, S, P), scanning the sheet and then typing the command is not very efficient.  Similarly, if you somewhat remember the function and have to think about it for 10 seconds, that's not very efficient either.  But if you know every function off the top of your head, you'll obviously operate much faster than others who need to refer to either their physical or mental cheat sheets.

The good news: all 3 of the aforementioned attributes can be significantly developed with the proper amount of repetition.  One year of banking analyst experience will yield roughly 5,000 hours of work, much of which is sadly just improving your computer skills through repetition.

So how fast is fast?  Well, Mrs. F-One can type 120 WPM.  That's pretty fast.  I can build a 3-statement model while using one hand to eat buffalo wings in less than 15 minutes.  Maybe you're not impressed, but given that I only type 80 WPM with TWO hands, that's not bad.  I've often mentioned to friends that if Mrs. F-One and I were to produce a child that gets all the right traits, this child would be the Lebron James of investment banking.  The other child would probably get cut from middle school basketball.  Anyway, I would gladly let Le-One go straight from high school to the pros.  The only part I want to avoid is Gloria James banging Delonte West in the team hotel.

I'm taking my talents to Wall Street...as soon as I unlodge this basketball from my dong.

There are obviously many ways to improve Excel speed, some of which I will discuss in future posts.  In the mean time, I strongly suggest 1) continuing to work hard while making an effort to memorize more functions/keystrokes and 2) http://www.freetetris.org/

Enjoy while Mrs. F-One gives me a beatdown for suggesting that our future child should become a banker,

F-One

Automatically Updating Page Titles for Sheets

Has anyone ever asked you how to automatically link a cell to the title of a sheet?  For example, if the current worksheet is called "Sheet1," how do you link to this name such that a change in the name will be reflected in your cell link?  More importantly, isn't it amazing how often a senior person asks you to do something in Excel without even being sure of whether it's possible or how the hell it could work?

You might be in the process of creating a product model in which there are 25 different products, and each product occupies a sheet within the model.  Let's say that you name each sheet for each different product, and have a title on each sheet that also matches the name of the product.  If you decide to change the nomenclature, you may be making 25 changes twice over (or even more than that, if you are using the product name in multiple cells on each sheet).

How do we link to sheet names?

Obviously, the more you link things together, the less manual updating you will need to do.  So here is a way to link to a sheet name, for whatever purpose you might need (make sure your file is saved on the hard drive).

1. Start with a formula that will return a string of text containing the sheet name.  Assume you are on "Sheet1."  You can go to cell B3 and enter: =+CELL("filename",$B$3), which returns "C:\Folder\[filename.xlsx]Sheet1"
2. Having the filepath and sheet name, you can create a function that returns only the part of this string of text that follows the "]," which would be "Sheet1"
3. One function that will work to return only the text following "]" is the RIGHT function: =+RIGHT(CELL("filename",$B$3),a) where a is the number of characters following "]"
4. Obviously, if all of your sheet names are 6 characters in length, you can just use the function from step 3 with a = 6,.  But a truly dynamic function will require solving for "a" in all cases.  So first, let's assume a = b - c, where b is the total length of the filename and c is the total number of characters through "]"
5. To find "b," use =+LEN(CELL("filename",$B$3)), which tells you that the filename is 31 characters in length
6. To find "c," use =+SEARCH("]",CELL("filename",$B$3),1), which tells you that "]" occupies the 25th position starting from the left in "C:\Folder\[filename.xlsx]Sheet1"
7. Using a = b - c, we have a = 31 - 26 = 5.  In formulaic terms, a = LEN(CELL("filename",$B$3))-SEARCH("]",CELL("filename",$B$3),1)
8. Thus, using the formulae from steps 3 and 7, the sheet name is =+RIGHT(CELL("filename",$B$3),LEN(CELL("filename",$B$3))-SEARCH("]",CELL("filename",$B$3),1))

Holy sheet!

-F-One

My Favorite Cousin: The F5 Key

 Keep going...keep going

Everyone knows that the fastest way to navigate to a random cell is entering the cell reference into the "Go To" menu.  In other words, if you want to get to cell AZ355, type: F5, AZ355, ENTER

Similarly, you know that if you have named a cell or cell range, you can select that name on this menu, and Excel will highlight the selection for you.

But what happens if you want to select some other group of cells that isn't named and isn't contiguous?  What if you're a first-year analyst who is being forced to color all of the hard inputs in a model to blue?  What if the model is 100 pages?  What if the penalty for forgetting to color one of the numbers is being called an idiot even though you sit next to an admin from Brooklyn that doesn't know how to read?

There is a solution for everything in Excel, and in this particular situation, it would be: F5, ALT + S, which brings you to the "Go To Special" menu.

...there!

At this menu, you can select "Constants" (ALT + O, ENTER), and then uncheck all of the boxes except "Numbers."  Now, you can highlight only the hard inputs in your model, and turn all of those numbers blue with just a couple of keystrokes, rather than selecting range after unbearable range and hoping you didn't miss anything along the way.

Step 1: Select a range

Step 2: Select criteria

Step 3: Only format these numbers...

Think of some of the other possibilities!  If you have hidden or grouped data that you do not want to format, you can select only visible cells and format those.  If you want to find out what cells are conditionally formatted, rather than trying to guess, you can do that easily.  In any case, my cousin F5 is extremely underutilized for how powerful it is.

Comments/questions welcome.

-F-One

Greetings!

Welcome!  Many (3) people have asked me to share my perceived wealth of excel knowledge with the rest of the world, so I have created this blog with the plan of regularly posting facts, "how-tos" and other updates on Excel for financial modeling and corporate finance in general.

What qualifications suggest that I can teach you, the reader, anything useful about Excel?  Well, I graduated from college (barely) in 2006 having taken one semester of an Excel class (B-), worked 3 years at a large investment bank, and currently work at a private equity firm.  So I have no legitimate credentials to support my case, but you can be the judges of whether my contributions are useful.  Here are some brief notes on the intended focus of this blog:

1. Formulas that improve the efficiency of financial modeling, data analyses and other commonly needed functions within Excel
2. Commands that improve efficiency, formatting and accessibility within Excel
3. I am currently using Excel 2007
4. Topics I do not intend to cover in-depth are: visual basic (not my expertise), statistics (my worst class in college), and pivot tables

The key word is efficiency.  Everywhere I have looked, there is someone using Excel less efficiently than they could, and in turn being less productive for no good reason.

As mentioned, the Excel information on this blog will be most relevant to corporate finance, particularly those people that work in investment banking (and related areas) and frequently use Excel.  But hopefully anyone looking to save some time or learn some interesting things about Excel will benefit.

If you need Excel help or have a topic you want to learn more about, feel free to leave a comment!

Thanks so much,

Mr. F-One